Converse Of Corresponding Angle Theorem

Definition: Corresponding angles are the angles which are formed in matching corners or respective corners with the transversal when ii parallel lines are intersected by any other line (i.east. the transversal). For example, in the below-given effigy, angle p and angle w are the respective angles.

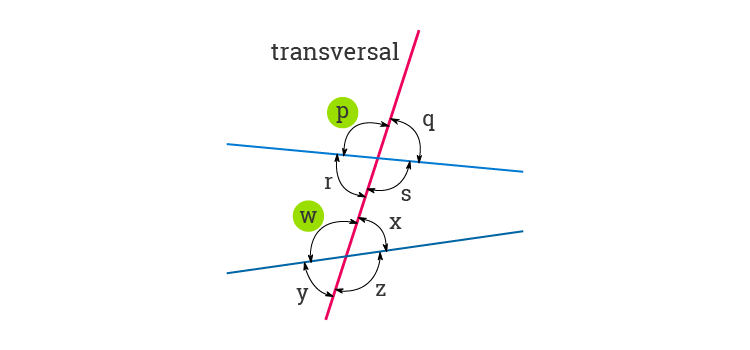
Corresponding Angles

Corresponding Angles Examples and Types

Examples of the corresponding bending are any angles which are formed on the contrary side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or 2 non-parallel lines. Thus, corresponding angles tin be of two types:

Corresponding angles formed past parallel lines and transversals
Corresponding angles formed past non-parallel lines and transversals

In Maths, you must have learned most different types of lines and angles. Here nosotros will talk over only corresponding angles formed by the intersection of 2 lines by a transversal. The 2 lines could be parallel or non-parallel. And then, allow us learn corresponding angles for both the cases.

Corresponding Angles Formed past Parallel Lines and Transversals

If a line or a transversal crosses any two given parallel lines, then the respective angles formed have equal measure. In the given effigy, you tin can come across, the ii parallel lines are intersected by a transversal, which forms 8 angles with the transversal. So, the angles formed past the start line with transversal have equal corresponding angles formed by the 2nd line with the transversal.

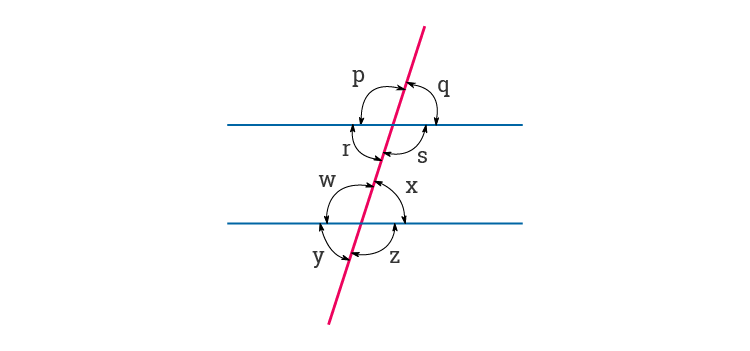
Corresponding Angles Formed by Parallel Lines and Transversals

All respective bending pairs in the figure:

∠p and ∠w
∠q and ∠x
∠r and ∠y
∠southward and ∠z

Note: The corresponding angles formed by two parallel lines are ever equal. So,

∠p = ∠westward

∠q= ∠x

∠r = ∠y

And ∠due south = ∠z

You should also note downwards, apart from corresponding angles, in that location are other angles formed when a transversal intersects two parallel lines. All the angles formed in the figure are:

Angle Blazon	Definition	Angle Relationships
Corresponding Angles	Angles formed at the aforementioned relative position at each intersection.	∠p = ∠westward, ∠q= ∠x, ∠r = ∠y, and ∠southward = ∠z
Vertically Contrary angles	The angles formed opposite to each other by a transversal.	∠p = ∠southward, ∠q = ∠r, ∠w = ∠ z and ∠x = ∠y
Alternate Interior Angles	The angles formed at the interior side or within the two parallel lines with a transversal.	∠r = ∠10 and ∠south = ∠west
Alternate Exterior Angles	The angles formed at the outside or exterior side of the 2 parallel lines with a transversal.	∠p = ∠z and ∠q = ∠y
Sequent Interior Angles/Co-interior Angles	The angles formed within the 2 parallel lines simply one side of the transversal is the sequent interior angles. The angles are supplementary to each other, that ways the sum of these 2 angles is 180°.	∠r + ∠west = 180° and ∠s + ∠x = 180°

Corresponding Angles Formed past Non-Parallel Lines and Transversals

For non-parallel lines, if a transversal intersects them, and then the corresponding angles formed doesn't have whatsoever relation with each other. They are not equal as in the instance of parallel lines only all are respective to each other.

Corresponding Angles Formed by Non-Parallel Lines and Transversals

Corresponding Angles Formed past Non-Parallel Lines and Transversals

In the aforementioned, there is no relationship betwixt the interior angles, exterior angles, vertically reverse angles and consecutive angles, in the instance of the intersection of ii non-parallel lines past a transversal.

Corresponding Angles Postulate

The respective bending postulate states that the corresponding angles are congruent if the transversal intersects two parallel lines. In other words, if a transversal intersects two parallel lines, the respective angles will be always equal.

Respective Angles in a Triangle

Corresponding angles in a triangle are those angles which are independent by a coinciding pair of sides of two similar (or congruent) triangles. Corresponding angles in a triangle take the same measure.

Corresponding Angles Theorem

The argument of the respective angles theorem states that "when a line intersects ii parallel lines, and so the corresponding angles in the 2 regions of intersection are coinciding".

Converse Of Respective Angles Theorem

The antipodal of the statement that "If the respective angles in the two regions of intersections are congruent, and so the lines are parallel in nature".

What happens when a transversal intersects the ii parallel lines and the set of corresponding angles are the same?

The 2 lines when intersected by a transversal are parallel. Information technology is the converse of the corresponding angle theorem.

Important Points On Respective Angles

In the case of two parallel lines intersected past a third one, the angles that apply the aforementioned relative position at every intersection are termed corresponding angles to one another.
The corresponding angles are coinciding in nature to one some other.
In the case where the respective angles in the 2 regions of intersections are congruent, then the two lines are parallel in nature.

Video Lesson on Types of Angles

Corresponding Angles Examples

Case 1: The two corresponding angles are given to exist 9x + x and 55. What is the value of x?

Respond:

The 2 given corresponding angles are congruent.

9x + 10 = 55

9x = 55 – x

9x = 45

10 = v

Instance two: The values of two corresponding angles are given to exist 7y – 12 and 5y + 6. What is the magnitude of each corresponding angle?

Answer:

The values of two corresponding angles are given to be 7y – 12 and 5y + vi.

To find the value of y.

The two given corresponding angles are congruent.

7y – 12 = 5y + half dozen

7y – 5y = 12 + 6

2y = xviii

y = 9

The magnitude of each corresponding bending,

5y + 6 = 5 (9) + 6 = 51

7y – 12 = vii * (9) – 12 = 51

Case 3: The values of two corresponding angles ∠1 = 3x + 1 and ∠v = 4x – iii. Solve for the value of 10.

Answer:

As they are corresponding angles and the lines are said to be parallel in nature, so they should exist coinciding.

Equate the given expressions ∠ane = 3x + 1 and ∠v = 4x – three and observe the value of x.

3x + 1 = 4x – 3

1 + 3 = 4x – 3x

4 = x

Hence the value of x is 4.

Case 4: The values of two corresponding angles ∠2 = 5x + two and ∠6 = 3x + 10. Solve for the value of x.

Answer:

As they are corresponding angles and the lines are said to be parallel in nature, then they should be congruent.

Equate the given expressions ∠2 = 5x + 2 and ∠6 = 3x + 10 and find the value of 10.

5x + 2 = 3x + 10

5x – 3x = 10 – 2

2x = viii

x = 8 / 2

x = iv

Hence the value of x is 4.

Example 5: The values of ii corresponding angles ∠7 = 5x + 5 and ∠three = 8x – 10. Solve for the value of 10.

Answer:

Every bit they are respective angles and the lines are said to be parallel in nature, and so they should exist congruent.

Equate the given expressions ∠seven = 5x + v and ∠3 = 8x – 10 and find the value of x.

5x + 5 = 8x – 10

five + x = 8x – 5x

15 = 3x

x = 15 / 3

x = 5

Hence the value of ten is 5.

Learn More than:

Subscribe to BYJU'Southward to get all the learning materials for Maths and Science bailiwick. Also, download its app to get personalised videos content.

Frequently Asked Questions

Can Corresponding Angles be Supplementary?

Respective angles can be supplementary if the transversal intersects two parallel lines perpendicularly (i.eastward. at 90 degrees). In such case, each of the respective angles will be 90 degrees and their sum will add up to 180 degrees (i.e. supplementary).

Are all Corresponding Angles Equal?

No, all respective angles are not equal. The respective angles which are formed when a transversal intersects 2 parallel lines are equal.

What is the Angle Rule for Corresponding Angles?

The angle rule of corresponding angles or the corresponding angles postulates states that the corresponding angles are equal if a transversal cuts two parallel lines.

Learn more than near corresponding angles here.

What are the Types of Corresponding Angles Based on their Sum?

Based on their sum, corresponding angles can be:

Supplementary Corresponding Angles (if their sum is 180 caste)
Complementary Respective angles (if their sum is 90 degrees)